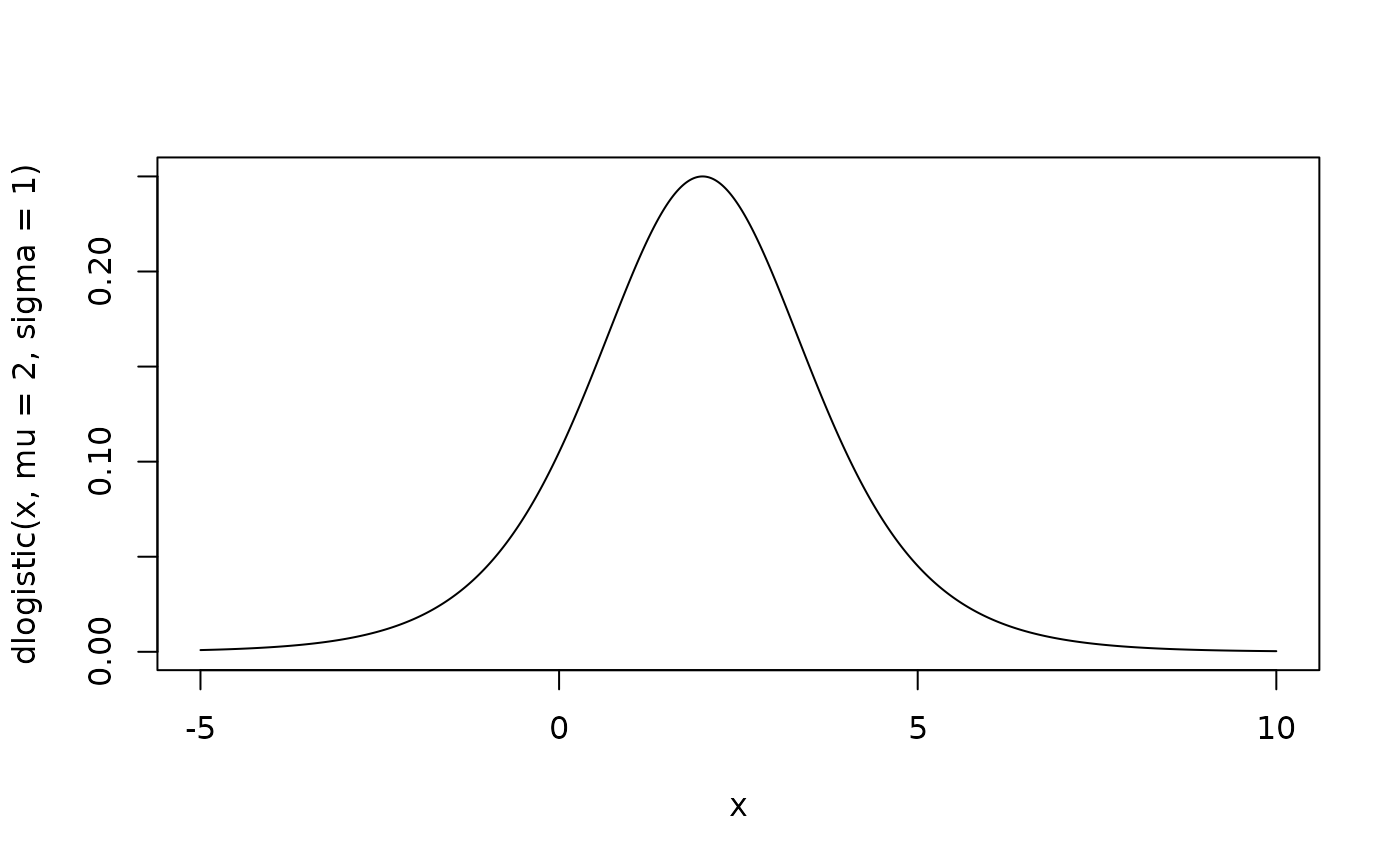
Probability density function for the logistic distribution
Usage
dlogistic(x, mu, sigma, log = FALSE)
Arguments
- x
Value, unbound
- mu
Mean, unbound
- sigma
Scale, sigma > 0
- log
Optional argument. If true, returns the log density.
Value
Density of the pdf given x, mu and sigma
Details
The logistic distribution has density
$$f(y | \mu, \sigma) = \frac{e^{-z}}{\sigma(1 + e^{-z})^2}$$
Where z is the linear transformation
$$z(y, \mu, \sigma) = \frac{y - \mu}{\sigma}$$
Examples
x <- seq(from = -5, to = 10, length.out = 1000)
plot(x, dlogistic(x, mu = 2, sigma = 1), type = "l")